今天与大家分享的内容是GPU加速的基于矩阵运算操作的图分析框架的设计与实现。

研究背景

GPU加速的基于矩阵运算操作的图分析框架这一研究问题的兴起，与GPU硬件的广泛使用以及图计算的发展息息相关。

GPU(Graphic Processing Unit)为大规模并行计算提供了硬件支持。尽管在其诞生初期，GPU仅仅是作为一种辅助加速图形渲染的专用硬件而存在，但是，进入新世纪以来，人们逐渐发现其SIMT(Single Instruction Mulitiple Threads)的运行逻辑以及高带宽的存储单元(GDDR, HBM等)同样能够应用于人工智能等对算力要求非常高的应用中。可以说，GPU的算力为人工智能的爆发提供了必要的基础设施。同时，广泛的、前途光明的应用场景也使得GPU器件的市场不断扩大，刺激相关厂商不断推陈出新。时至今日，GPU已经被应用于人工智能、科学计算、数值模拟等众多领域，成为了高性能计算应用中不可或缺的硬件。越来越多的研究者也试图针对其高算力高带宽的的特点，在不同的研究问题中加以利用。

图计算就是一类适合使用GPU加速的热点研究问题。图(graph)使用结点表示现实世界中的实体或事件，使用结点之间的边表示其之间的相互关系。图及其分析算法具有强大的表达能力和灵活性，已经在金融、生物化学、社交网络等多种领域得到应用。目前图计算的一大问题是，当图规模不断扩大时，现有方法的代价也随之扩大。GPU具有高并发、高带宽的特点，利用GPU进行图计算加速是一种可能的解决办法。

研究动机

本文主要聚焦GPU加速的基于矩阵计算的图计算框架。

图计算框架为用户提供构建图分析算法的基本算子，并为用户提供底层操作的高效实现。图计算框架是一个被研究已久的课题，现有的图计算框架，大致可以分为三种类型。

其一是点中心(vertex-centric)的图计算框架，顾名思义，它将计算负载按照结点进行划分，分配给各个工作单元(e.g. 线程，线程组，进程)。谷歌提出的Pregel[2]是点中心图计算框架最早的实践之一，它以点为单位并行，并使用BSP同步。Pregel在大规模图上表现出一定的性能劣化，具体表现在大直径图收敛慢和大规模图负载不均衡。PowerGraph[3]首次将GAS模型引入了点中心的图计算框架，在保持以点为单位并行的基础上，GAS 将顶点上计算的过程明确地分割成了Gather，Apply，和 Scatter 三个步骤。Gather规约当前顶点通过边收集到的信息，Apply将Gather阶段地结果应用到当前顶点上，Scatter阶段，根据Apply阶段的结果，将当前顶点的最新结果更新到该顶点的边上。Pregel与PowerGraph都是点中心的图计算框架的早期实践，但是为后期的大量工作打下了基础。

其二是边中心(edge-centric)的图计算框架。与点中心的图计算框架相反，它将边作为并行的基本单位，将图理解为以流形式不断到达的边的集合。X-stream[4]最早实现了边中心的图计算框架。这类框架在处理动态图数据以及增量算法上有得天独厚的优势。

其三是本文重点关注的基于矩阵计算的图计算框架。早期工作表明，绝大多数图分析算法都可以表达为对图的邻接矩阵的计算，因此，基于矩阵计算的图计算框架需要关注高效的矩阵计算实现即可。其中，CombBLAS[5]定义了基于矩阵计算的图计算算子，GraphMat[6]对用户暴露点中心的API，自动将用户逻辑转换为矩阵计算,GBTL[7]给出了一种GraphBLAS API的GPU实现，而GraphBLAST[8]则提出了更加完善的实现方案与优化。

利用矩阵计算实现GPU加速的图计算框架有其可行性。首先，矩阵计算的性能在GPU上经过了长时间的探索与优化。目前有大量针对不同应用场景的矩阵计算库可供使用。矩阵计算本身也更加适合GPU的并发执行模型。其次，各种图分析算法被严格的数学证明能够使用矩阵操作来进行表达。例如下图中的图宽度优先遍历中，从红色的3号点通过一次迭代拓展到紫色的0号和2号点的过程可以表示为右图中的矩阵计算。其中A为图的邻接矩阵，向量x表示当前需要进行扩展的点，即3号点的位置为1，其他位置为0。矩阵与向量的乘积即为拓展后的点，即0号点与2号点。

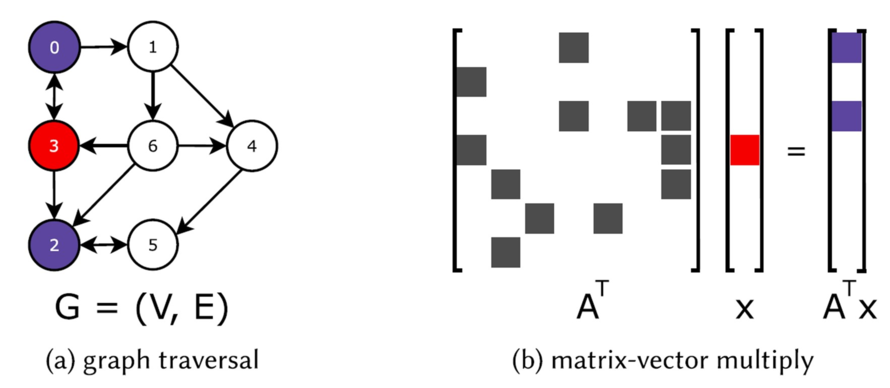
尽管如此，利用矩阵计算实现GPU加速的图计算框架也存在三个挑战：(1)因为图的邻接矩阵通常具有稀疏与不均匀的特点(在真实世界图数据中尤甚)，所以不同结点产生的工作负载并不均衡。并且稀疏矩阵运算本身也比稠密矩阵计算对GPU的负载不均更加严重。(2)许多图算法中计算本身的开销较小，使得算法没有足够的工作量来打满GPU中的计算资源，一个GPU上的计算kernel的实际运行时间很短，但kernel的初始化、同步以及内存分配都需要额外的时间。在一些极端情况下，这些额外时间甚至超过了kernel本身运行的时间。(3)图计算的访存计算比较低。即一次访存后需要执行的计算较少。kernel执行中的大部分时间都消耗在从非结构化数据中读写上，这使得图算法在GPU上的瓶颈落在访存上，而GPU的访存上限比计算上限更容易达到。

代表工作

下面本文将介绍利用矩阵计算实现的图计算框架的两个代表工作：GraphMat与GraphBLAST

GraphMat: High Performance Graph Analytics Made Productive

GraphMat的主要贡献为，它是第一次将用户友好的点中心的图计算框架与基于矩阵运算的图计算算法底层实现连接在一起，并且在多核架构上进行了优化。使用GraphMat的开发者不需要学习矩阵计算的相关知识，而是可以沿用其较为熟悉的点中心的编程范式。相关论文发表在VLDB 2015上。

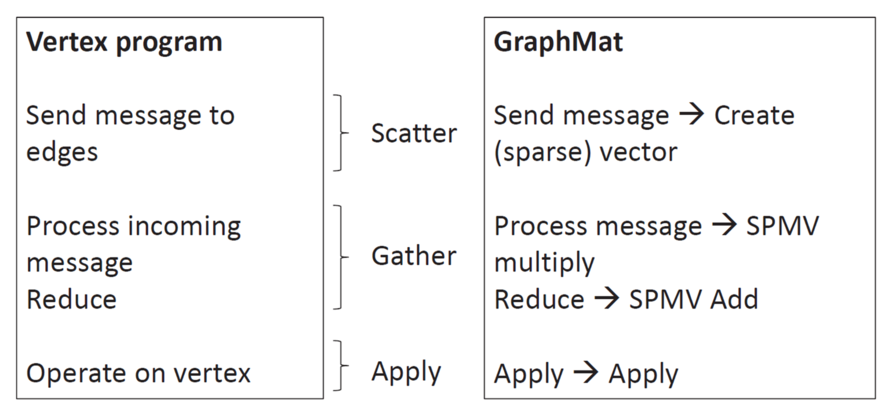
GraphMat中点中心的图计算框架仍然采用GAS模型，其与底层的矩阵计算的对应关系如图所示。Scatter操作为通过边发送消息，对应的矩阵操作为创建向量。Gather操作为对从边传递过来的消息进行处理，对应的矩阵操作为矩阵乘法以及按位计算操作。Apply操作为更新当前顶点的信息，在矩阵操作中对应的是对矩阵中的元素进行修改。

算法1为GraphMat中提出的矩阵运算的SPMV(Sparse Matrix Vector Multiply)计算方式。其中，图G的邻接矩阵是稀疏矩阵，其存储形式为CSC(Compressed Sparse Column)。CSC与图计算中常见的CSR结构类似，它按列存储稀疏矩阵中的非零元素以压缩稀疏矩阵的存储空间，并提供高效的按列访问模式。具体而言，在执行SPMV时，需要按列遍历G中的非零元素，并将其与稀疏向量中的对应位置进行匹配。

GraphMat关注的另一个重点问题是稀疏矩阵与稀疏向量的存储。对稀疏矩阵，它引入了双层CSC结构DCSC。DCSC把column index分成chunk，AUX记录每个Chunk里非零元素数量的前缀和，一个chunk一般是，这是为了节掉省全零的列的offset，并且行遍历比CSC快。而对稀疏向量，它采用了两种方式，一是将其中非零元素存储为的tuple集合，并通过index顺序存储;二是使用一个bitvector记录非零元素的位置。存tuple好处是节省空间，bitvector好处是能够根据缓存行进行对齐，并且在存储上较为规整。,value>

从实验结果中不难发现，GraphMat与此前的方法相比有较大的性能提升。比GraphLab平均快5.8x， 比CombBLAS平均快6.9，比Galois平均快1.2，但TC(三角形计数)和SSSP(单源最短路径)更慢，而PageRank算法上的优势最为明显。

GraphBLAST: A High-Performance Linear Algebra-based Graph Framework on the GPU

GraphBLAST的相关论文发表在期刊TOMS 2022上。其主要贡献为提供了一种GraphBLAS API在GPU上的高效实现。它提出了一个代价模型来选择不同的算法以处理不同稀疏程度的矩阵和向量。它还第一次考虑到了输出数据的稀疏性，引入了一种masking的实现方法。最后，它在访存模式和负载均衡上也提出了相关的优化方法。

GraphBLAST的框架层次如图所示。它兼容C++编程语言，为用户提供IO、算法和测试的接口。在底层它实现了GraphBLAS API，能够支持CPU和GPU两种底端实现。

GraphBLAST首先探究了输入数据的稀疏性对算法的影响。在图计算框架中有frontier的概念。它是指在上一次迭代中刚刚访问到的点集合，也是在当前迭代中需要进行拓展的点的集合。在先前工作中，研究人员在BFS的基础上(后续工作中拓展到了一般情况)提出了frontier的两种拓展模式：Push与Pull。Push就是从当前的frontier出发，访问其中的点的邻居，并维护visited数组，得到下一轮的frontier。Pull就是反其道而行，从当前未visited的点出发，查询其邻居是否在当前的frontier中，如果在，那这个点标记为visited，并且在下一轮的frontier中。所谓Direction optimization是指在最初的时候和快结束的时候，frontier里的点比较少，适合用push，在中间的迭代轮次的时候，frontier里的点很多，适合用pull。从矩阵计算的角度理解，这实际上是指在SpMSpV与SpMV中进行选择[9]。其区别就在于将输入向量按照稀疏向量或是稠密向量的形式来计算。

如上图中所示，(a)将向量表示为稠密向量，这时执行乘法需要遍历邻接矩阵的每一行，来得到结果。而(b)将向量表示为稀疏向量，只存储其中的非零元素。这时执行乘法只需要遍历非零元素对应的非零列。与(a)中的SpMV计算逻辑相比，(b)中的SpMSpV方式能够节省访存代价，但相应地SpMSpV的负载均衡需要优化。因此，在(c)中可以看到，SpMSpV性能在向量中非零元素较少时优于SpMV。而SpMV的性能基本与向量中的非零元素个数无关。

除了输入向量以外，输出的稀疏性也对图计算框架实现有影响。在不同的图算法中，通常需要对结点进行某种过滤和选择。GraphBLAST将这一操作称为masking操作：在不同的算法中，masking可以用来实现不同的步骤。例如，BFS中，对visited数组进行检查可以实现成masking，在SSSP中，masking可以用于将在这一轮中被更新的active的结点筛选出来，在PageRank中，可以用于判断每个点的PR值是否收敛。

GraphBLAST讨论的核心问题是masking应当在矩阵计算之前作用在邻接矩阵上，或是应当在矩阵计算之后作用在计算的输出矩阵/向量上。如下图所示：

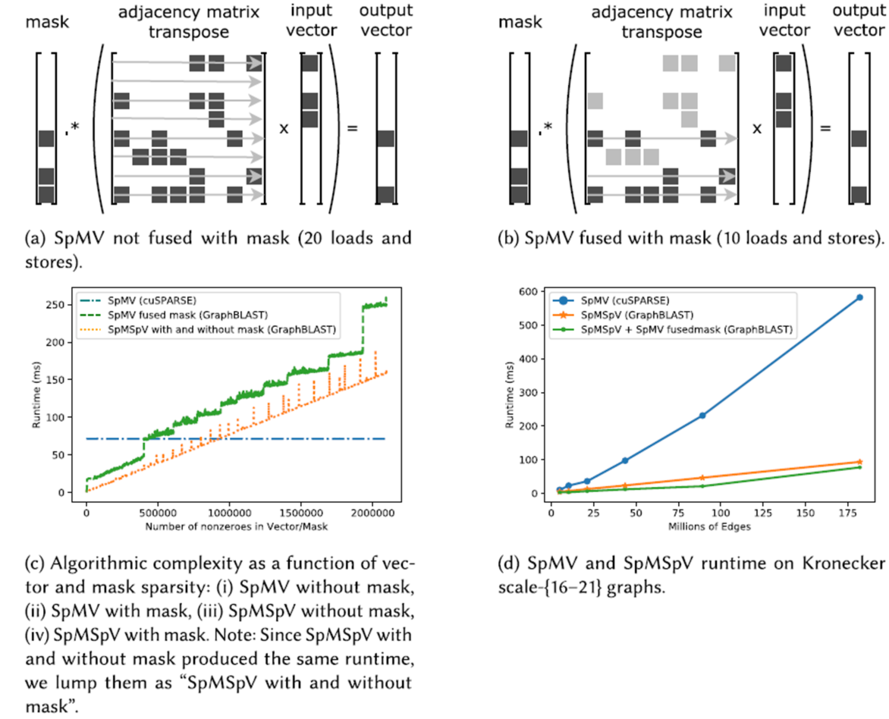
(b)中的计算方式下，在矩阵与向量做乘法时只需要遍历masking向量中标记为有效的行，从而减少访存代价。与此前关于SpMSpV与SpMV的分析结果类似，当masking向量足够稀疏时，将masking操作提前能够带来性能的提升。而与此前不同的是，由于提前masking能够减少中间结果的规模，所以还能够节省矩阵操作的空间消耗。

GraphBLAST关注的第三个重点问题是在SpMV与SpMM中的负载均衡。

执行SpMV和SpMM的时候，主要影响负载均衡的关键是怎么划分一个稀疏矩阵，来分配给各个线程。文中主要讨论三种方法。

第一种是行划分的方法，这个方法简单粗暴，将带有非零元素的行分均分配给各个线程，这个图里黄色的点就是工作负载划分的分界点，可以看到不同线程负责的非零元素的个数是有差异的。

第二种是基于merge的方法，跟第一种方法相反，它把非零元素平均分配给各个线程，然后通过二分搜索找到每个线程负责的非零元素的最小行号。这种方法更加平衡，但是引入了log级别的额外开销。

第三种是基于merge path的方法，具体做法是将row_ptr和A.val两个作为列表执行归并，然后将这条路径上的点平均分配给每个线程，然后找到切分点的下标。这种做法能够使得行和非零值都比较平均。

如上图所示，对SpMV而言，merge-based在大部分情况下都要好于Row split，这里原文的图有个错误，图例和图里的折线颜色反过来了。这里注意单位Gflops的s是小写，所以应该是指计算量而不是吞吐量，所以是越小越好。

Row split容易造成不均匀的问题在每行的非零元素不均匀或者特别稀疏的时候更加明显。因此，对SpMV，GraphBlast采用的是基于merge的划分，对SpMM，当平均每行的非0元素个数小于9.35时，使用merge，否则使用row split

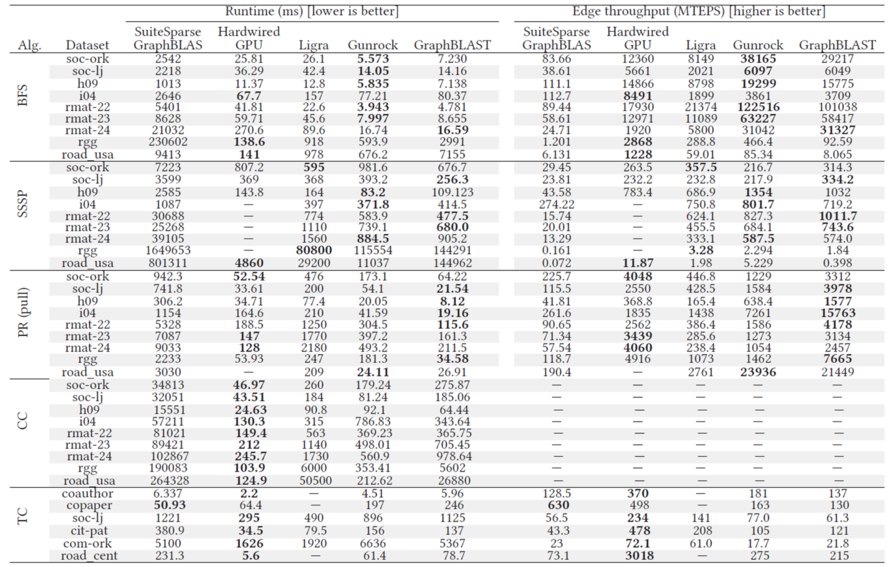
在实验部分，SuiteSparse和ligra是CPU上的系统，Gunrock是GPU上的框架，Hardwired GPU是指针对特定算法写的GPU实现。可以看到的是GraphBlast在pagerank上优势最大，有快一个数量级，在三角形计数，弱联通分量上并不理想。

1. Yang, D., Liu, J., Qi, J., & Lai, J. (2022). WholeGraph: A Fast Graph Neural Network Training Framework with Multi-GPU Distributed Shared Memory Architecture. SC22: International Conference for High Performance Computing, Networking, Storage and Analysis, 1-14.

2. Grzegorz Malewicz, Matthew H. Austern, Aart J. C. Bik, James C. Dehnert, Ilan Horn, Naty Leiser, and Grzegorz Czajkowski. 2010. Pregel: A system for large-scale graph processing. In Proceedings of the 2010 ACM SIGMOD International Conference on Management of Data (SIGMOD’10). 135–146

3. Joseph E. Gonzalez, Yucheng Low, Haijie Gu, Danny Bickson, and Carlos Guestrin. 2012. PowerGraph: Distributed graph-parallel computation on natural graphs. In Proceedings of the USENIX Conference on Operating Systems Design and Implementation (OSDI) (OSDI’12). USENIX Association, 17–30.

4. Amitabha Roy, Ivo Mihailovic, andWilly Zwaenepoel. 2013. X-Stream: Edge-centric graph processing using streaming partitions. In Proceedings of the Twenty-Fourth ACM Symposium on Operating Systems Principles - SOSP’13. ACM Press, 472–488

5. Aydın Buluç and John R. Gilbert. 2011. The Combinatorial BLAS: Design, implementation, and applications. The International Journal of High Performance Computing Applications 25, 4 (Nov. 2011), 496–509.

6. Narayanan Sundaram, Nadathur Satish, Md Mostofa Ali Patwary, Subramanya R. Dulloor, Michael J. Anderson, Satya Gautam Vadlamudi, Dipankar Das, and Pradeep Dubey. 2015. GraphMat: High performance graph analytics made productive. Proceedings of the VLDB Endowment (VLDB) 8, 11 (July 2015), 1214–1225.

7. Peter Zhang, Marcin Zalewski, Andrew Lumsdaine, Samantha Misurda, and Scott McMillan. 2016. GBTL-CUDA: Graph algorithms and primitives for GPUs. In IEEE International Parallel and Distributed Processing SymposiumWorkshops (IPDPSW). IEEE, 912–920

8. Yang, Carl et al. “GraphBLAST: A High-Performance Linear Algebra-based Graph Framework on the GPU.” ACM Transactions on Mathematical Software (TOMS) 48 (2019): 1 - 51.

9. Maciej Besta, Michał Podstawski, Linus Groner, Edgar Solomonik, and Torsten Hoefler. 2017. To push or to pull: On reducing communication and synchronization in graph computations. In Proceedings of the 26th International Symposium on High-Performance Parallel and Distributed Computing. ACM, 93–104.