1 引言
目前,关于疲劳寿命的估算方法基本上是两种,即基于试验的S-N曲线法和基于疲劳裂纹扩展的断裂力学方法。多数国家采用S-N曲线法,但挪威船级社等已把断裂力学方法和S-N曲线法都列入规范作为疲劳寿命估算的分析方法。S-N曲线法具有广泛的可用性,而断裂力学方法是一个更合适的方法。因为断裂力学方法可以比较真实地模拟构件表面裂纹从萌生至扩展失效的全过程,而且所需的投资远比基于大量模型试验的S-N曲线法少,因此,它已逐渐成为各国疲劳断裂研究的主要发展方向。
为了进一步探明三维表面裂纹在疲劳载荷下的扩展规律,本文对于含半椭圆三维表面裂纹在等幅拉伸载荷作用下的扩展,特别是疲劳裂纹扩展过程中其形状的变化规律进行探讨,与理论公式进行对比分析,获得了一种推导疲劳裂纹扩展过程中裂纹形状的有效方法。
2 三维表面裂纹扩展的理论推导
为了计算出裂纹扩展过程中半椭圆形裂纹的深度和表面半长度之比![]() 的变化规律,如图1所示对裂纹深处A和表面处C分别应用Paris裂纹增长公式,得到:
的变化规律,如图1所示对裂纹深处A和表面处C分别应用Paris裂纹增长公式,得到:
![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
式中:![]() 分别为裂纹表面C和深处A的应力强度因子幅值。由式(2.1),(2.2)可以得到:
分别为裂纹表面C和深处A的应力强度因子幅值。由式(2.1),(2.2)可以得到:
![]() (2.3)
(2.3)
通过对式(2.3)的积分就可以得到半椭圆形裂纹的深度和表面半长度之比![]() 的变化规律。三维表面裂纹的应力强度因子K虽有几个可行的表达式,但目前被广泛应用的是Newman-Raju公式:
的变化规律。三维表面裂纹的应力强度因子K虽有几个可行的表达式,但目前被广泛应用的是Newman-Raju公式:
![]() (2.4)
(2.4)
式中,![]() 分别为拉伸、弯曲正应力,H、F是以裂纹相对深度a/t、裂纹形状比a/c 、离心角
分别为拉伸、弯曲正应力,H、F是以裂纹相对深度a/t、裂纹形状比a/c 、离心角![]() 等为参数的修正系数, 为第二类椭圆积分。
等为参数的修正系数, 为第二类椭圆积分。
Newman和Raju在实验的基础上引入了![]() 和
和 ![]() 之间的关系:
之间的关系:
![]() (2.5)
(2.5)
再将A、C点的应力强度因子代入式(2.3)中去得到[1]:
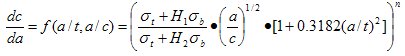 (2.6.1)
(2.6.1)
文献[2]在 ![]() =
=![]() 的情况下得到:
的情况下得到:
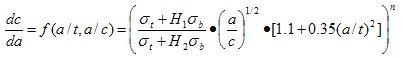 (2.6.2)
(2.6.2)
对于(2.6.1)和(2.62)式的求解要采用数值积分的方法进行。
记:x=a/t ,y=a/c ,则(2.6.1)、(2.6.2)式的变换过程为:a=xt ,c=a/y=xt/y ,![]() ,考虑到厚度t为一个常数,(2.6.1)和(2.6.2)式可以进一步写为:
,考虑到厚度t为一个常数,(2.6.1)和(2.6.2)式可以进一步写为:
移项变成: ![]() (2.7)
(2.7)
当初始裂纹形状比、相对深度和裂纹扩展的材料常数已知时,由上式可求得各种载荷下裂纹形状变化规律。对式(2.7)的数值积分结果得到 a/c和a/t 之间的关系,于是式(2.4)的应力强度因子K就仅是a/t 的函数,对于式![]() 的积分就可以进行下去,直至裂纹深度达到破坏值,这样就得到疲劳裂纹扩展的寿命以及裂纹的扩展形状。
的积分就可以进行下去,直至裂纹深度达到破坏值,这样就得到疲劳裂纹扩展的寿命以及裂纹的扩展形状。
3有限元计算
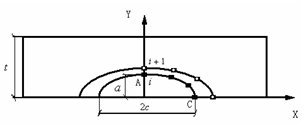
(a)两自由度裂纹扩展计算模型
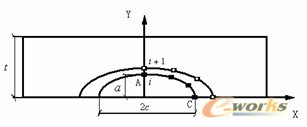
(b) 多自由度裂纹扩展计算模型
图1 半椭圆形状的裂纹扩展模型
图1所示含表面裂纹构件裂纹扩展计算的两种计算模型[3],即:两自由度裂纹扩展模型和多自由度裂纹扩展模型。两自由度模型的基本计算过程是:在A、C两点应用Paris公式计算裂纹增长量,假设表面裂纹在扩展过程中沿裂纹线的法线方向保持半椭圆形状,但是半椭圆形裂纹的深度和表面半长度之比a/c之比将发生变化,并不保持为常数。本文以平板模型为例,如图2所示,计算过程与其他方法所不同的是通过给定裂纹深度方向扩展增量,利用ANSYS软件求出A、C两点的应力强度因子,然后再利用paris公式计算表面半长度,获得疲劳裂纹扩展的形状变化规律。


