【IT168 技术】一.为何要在大规模SNS中挖掘兴趣圈子
随着国外的facebook、twitter以及国内的人人、新浪微博等SNS及内容分享平台的逐步流行,如何从上亿的海量用户中自动挖掘兴趣圈子成为了一个有趣也非常必要的工作。所谓“兴趣圈子”,指的是在同一分享平台下,有着共同的兴趣爱好的用户群体,比如新浪微博里哪些用户是对云计算感兴趣的?他们是否形成了一个密切交互的圈子?对这些信息的挖掘是很有趣也很有实际用处的。
如果能够从海量用户中通过自动手段挖掘出一个个的兴趣圈子,对于很多具体应用来说是非常重要的基础数据,比如可以利用用户所属兴趣圈子进行感兴趣人物推荐,或者根据所属圈子的群体特性分析用户的个人兴趣点等,所以在SNS平台下,如何对海量数据自动进行兴趣圈子挖掘是个非常有用的基础功能。
二.如何挖掘兴趣圈子
现在的问题是:给定海量用户,如何才能挖掘出具有相似兴趣的圈子?我们基于微博用户的互动信息,构建了一整套兴趣圈子挖掘算法,并取得了较好的挖掘效果。如果把每个用户想象成一个巨大的图中一个节点,如果用户A对用户B有互动行为(转发,评论等),我们可以在用户A和用户B之间建立一条有向边,通过这种方式可以构建出有上亿节点,几十亿边的巨大的有向图。挖掘兴趣圈子就是在这样的巨图中进行的。我们把兴趣圈子挖掘转换为一个图切割问题的具体应用。图1是这个思路的简化图示例。
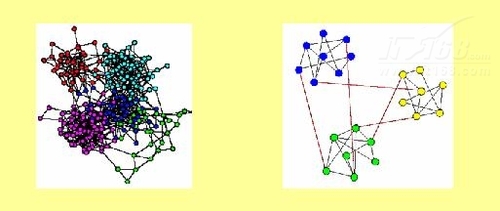
▲图1 兴趣图例子
2.1 图切割问题
图切割问题本质上是一个聚类问题,几乎所有聚类算法的基本思想都是相近的:给定一批数据,自动对数据进行聚类,使得聚合到同一类别的数据之间比较相似,而不同类别之间的数据差异较大。图切割问题也符合这个定义,等于是将图中节点进行聚类,把密集相连的一批节点聚合到一起,而连接比较稀疏的节点尽可能划分到不同的类别中。
如果用相对形式化的语言来描述的话,图切割问题就是:给定n个点(x1, x2…,xn),聚类的目标是将这n个点分成k个簇,使得同一簇中的数据点比较相似,不同簇间的数据点比较相异。如果按照节点之间的兴趣相似度构建关系图G(V, E),问题就转化为了在图G上做划分,将图G分成k个子图A1,A2,…Ak,使得划分后子图内包含边的总权值尽可能高,而子图之间边的权重尽可能小。在图1所示的例子中,标为相同颜色的节点可被视为聚合到相同子图中,边的权值直观表示为边的长度,即边越长,两个节点距离越远,即其相似性越小,也就是说其边的权值小。
图切割算法有很多,比如min-cut,min-max cut,ratio cut等等,我们采用了谱聚类算法来挖掘用户兴趣圈子。
2.2谱聚类算法
谱聚类算法和很多其他距离算法相比有很多优点,下文会详述此点,同样的,谱聚类也适合解决图切割问题。
谱聚类有个比较有趣的特性,即这个算法可以将图切割问题转换为求由图形成的矩阵的特征值和对应的特征向量问题,这样就把图切割问题转换为矩阵特征值求解及在其基础上的聚类问题。
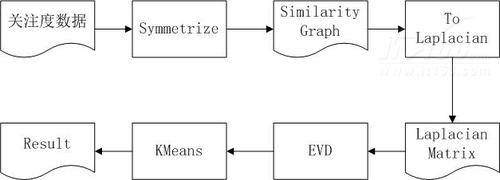
▲图2 谱聚类算法流程
图2是利用谱聚类进行兴趣圈子挖掘的算法流程示意图,首先我们获得用户之间的互动数据,由于谱聚类只能处理无向图,而用户之间的互动数据是有向的,所以首先根据一定规则将有向图转换为无向图,之后就形成了所有用户的兴趣相似性图。根据谱聚类算法要求,将这个相似性图转换为拉普拉斯矩阵,然后对这个矩阵求其前K个特征值及其对应的特征向量,求解前K个特征向量s1,s2,…,sk,组成矩阵S[n][k](n为用户编号),这样就将一个原本是n*n的矩阵转换为小很多的n*k矩阵,对S按行进行Kmeans聚类,每一行对应相似兴趣图中一个节点。其最终聚类结果就是谱聚类最终的输出结果。
之所以采取谱聚类来解决这个问题,源于这个算法本身具有的一些优点,比如:
·谱聚类具有坚实的理论基础:图谱理论
·谱聚类不含凸球形数据分布的隐性假设,而常见的很多聚类算法比如KMeans, EM算法都存在这一假设。比如对于图3所示的例子中,谱聚类的聚类效果比较好。
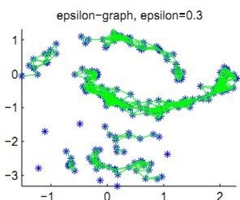
▲图3 非凸球形数据
由于谱聚类具备独特的优点,所以近来应用非常广泛(语音识别、文本挖掘等),但是谱聚类的计算复杂度还是较高,所以面对海量数据,如何能够快速计算是个问题。
为了能够处理上亿的海量数据,我们主要采取了两项措施来对原始算法进行改造,首先是利用MPI平台构建分布式计算系统,对于这种计算密集型迭代式应用,通常hadoop平台被认为是不太合适的,所以通过构建MPI分布式平台来加快数据的分布以提升计算速度。
第二项主要改进措施是将谱聚类由平面型聚类(flat)改造为层次聚类(hierarchy),其基本思想也很简单,即通过多次谱聚类迭代,首先将一个巨大的图划分为较少数的密集子图,然后针对每个密集子图再次迭代使用谱聚类来递归地将其划分为较小的密集子图,通过几个层级的切割,也可以有效增加分布式计算效果并大大提快整体运行效率。
当然,除了以上两项主要改进措施,还包含一些相对细小的改进,在此就不赘述细节了。


